Fundamentos para racionalizar um debate

Pense em uma questão sob intenso debate hoje. Pode ser algo de ampla relevância, digamos, uma proposta política que impactará o futuro do seu país ou um assunto mais local e corriqueiro, como uma decisão de condomínio. O importante é que, independentemente da temática, você perceba que há de fato um debate e dois ou mais grupos têm posições conflitantes a respeito do que deve ser feito.

Agora examine qual a sua opinião pessoal sobre a questão. Talvez um dos grupos represente  integralmente o que você pensa. Talvez apenas partes do que alguns dos grupos defendam combine com sua posição. Ou talvez nenhum deles faça sentido. Qualquer que seja a situação, pergunte-se: tenho certeza de que a posição que defendo está absolutamente correta? Se a resposta for “sim”, parabéns. Mas trago más notícias: você provavelmente não fará um bom papel em um debate sério.

A dúvida é um elemento central no método científico, talvez o melhor método já encontrado pela humanidade para resolver questões complexas e multifacetadas. Richard Feynman, físico americano vencedor do prêmio Nobel em 1965, defendia que reconhecer a própria ignorância e deixar espaço para a dúvida são condições essenciais para o progresso. A ciência, segundo ele, é formada por um conjunto de afirmações com diferentes graus de certeza: temos mais segurança em algumas constatações do que outras, mas nenhuma afirmação vem com absoluta certeza atrelada. O que hoje parece sólido, amanhã pode ser demonstrado incorreto.

Ao primeiro olhar, há um grande contraste entre palavras de Feynman e o debate contemporâneo na internet. Não é difícil perceber como as redes sociais deram alcance e promoveram a difusão do debate irracional. Mas a desonestidade intelectual está longe de ser uma invenção moderna. Em 1831, por exemplo, o filósofo alemão Arthur Schopenhauer já publicava o satírico “Como vencer um debate sem precisar ter razão”. Quase dois séculos depois, trechos de debates rasos retirados da internet, muitas vezes feitos por meio de frases prontas, memes e ofensas, poderiam ser usados para compor uma versão ilustrada da obra.

O cenário não é dos melhores, mas nem tudo está perdido. Ainda que timidamente, comunidades virtuais tem surgido com a proposta de fomentar o franco embate de ideias visando o aprendizado de todas as partes. Frequentemente, tais grupos buscam discutir como estamos condicionados a cometer repetidamente os mesmos erros lógicos – os vieses cognitivos – além de promover um pensamento bayesiano, isto é, estar disposto a mudar de opinião frente a novas evidências. Alguns bons exemplo são o Change My View, em que usuários requisitam e avaliam argumentos que o façam mudar de opinião, e o Less Wrong, que inclusive organiza reuniões presenciais de debate e estudo entre os membros.

Afirmações científicas têm algo em comum

A noção de que novas evidências podem modificar a forma como encaramos uma determinada questão é central na formação de afirmações científicas e as diferenciam de outras afirmações. Em termos mais precisos, conforme popularizados pelo filósofo austro-britânico Karl Popper, hipóteses científicas são falseáveis ou passíveis de refutação. Se não é possível conceber um fato que contradiga uma asserção, estamos lidando com uma afirmação não-científica. Fora do mundo acadêmico, entretanto, e de volta para o debate do dia-a-dia, nem sempre as evidências são suficientemente fortes ou críveis para derrubar nossas teses internas. De uma forma menos abrupta, podemos encarar nossas opiniões como resultado do acúmulo de evidências pró e contra nossas hipóteses. Bayes entra em cena.

A regra (ou teorema) de Bayes pode ser usada para descrever como novos fatos afetam o grau de certeza de hipóteses. Se um evento que julgávamos improvável ocorre com uma frequência que nos surpreende, geralmente reavaliamos nossa opinião inicial. Por exemplo, João acredita que seu carro está em bom estado de conservação e, portanto, deve apresentar em média um problema mecânico por ano. Se em um semestre o carro de João quebrar 6 vezes, ele certamente reavaliará sua afirmação inicial e terá menos certeza do bom estado de seu carro.

Por ser um teorema matemático, a regra de Bayes é expressa em notação formal. Por mais que pareça frio e abstrato, essa caracterização pode aproximar de maneira razoável a maneira como seres humanos absorvem novas informações. Em uma recente pesquisa [1], o professor Seth Hill, do Departamento de Ciências Políticas da Universidade da Califórnia, San Diego, estudou como as pessoas aprendem coletivamente a respeito de fatos políticos. Os resultados mostraram que em 70% dos casos os sujeitos reavaliaram suas certezas exatamente como previsto pela regra de Bayes.

Um dos benefícios da linguagem matemática é a precisão de significado, o que muitas vezes possibilita a obtenção de valiosos insights derivados logicamente (por exemplo, veja esse outro artigo publicado aqui). Tendo isso em mente, o exemplo a seguir apresenta uma aplicação simplificada da regra de Bayes para mostrar como a dúvida é importante no aprendizado. Caso o leitor não se sinta atraído por esse tipo de exercício pode tranquilamente pular para a conclusão.

Ausência de dúvidas impede a atualização: Bayes na prática

Imagine que a cidade de João esteja implementando mudanças significativas para combater o elevado trânsito nas estreitas ruas do centro da cidade. O novo sistema transformará as avenidas que circulam o centro em vias de mão única, forçando motoristas que transitam entre as várias regiões da cidade a trafegar ao redor do centro ao invés de cruzá-lo. A hipótese aqui pode ser definida como “o novo sistema reduzirá o problema de congestionamento no centro da cidade”. Considere que “V” representa o evento de que essa afirmação é verdadeira e “F”, falsa.

João desconfia dos planos e da competência da prefeitura e acredita que o novo sistema trará mais problemas do que resolverá. Ele acredita que há apenas 30% de chances de o plano dar certo (ou, em outra forma de ver, ele tem 70% de confiança na posição de que o novo sistema não melhorará o trânsito). Formalmente, podemos escrever Probabilidade(F) ou Pr(F) = 70% e Pr(V) = 30%. Essas são as probabilidades a priori.

Sabe-se que um relatório do Departamento de Trânsito será divulgado um mês após as mudanças entrarem em vigor. João também não confia muito na isenção do Departamento e acha que eles podem ter uma visão parcial na análise dos dados, que podem inclusive ter sido coletados de forma inadequada e levarem a conclusões erradas. Considere que há apenas duas possibilidades de relatório: favorável (chamemos de evento P) e desfavorável (N) às mudanças.

Assim sendo, João considera que as chances de o relatório ser favorável às mudanças quando elas são de fato benéficas (V) são de 95%. Matematicamente, representamos isso como Pr(P|V) = 95%, e lemos como “probabilidade do evento P dado V”. Por outro lado, João considera que mesmo que as mudanças não ajudem a resolver os problemas de congestionamento, a parcialidade do Departamento faria com que o relatório fosse favorável em 50% dos casos: Pr(P|F)=50%. (As probabilidades do evento alternativo são: Pr(N|V) = 5% e Pr(N|F)=50%).

Com esses dados, temos os elementos necessários para avaliar como uma nova evidência (relatório) afeta a posição de João com relação às mudanças. Nesse caso, queremos saber qual o grau de certeza de João após a divulgação do relatório positivo: Pr(V|P), também chamada de probabilidade a posteriori. Pela regra de Bayes:

Substituindo os valores, temos:

Ou seja, um relatório positivo atualizará os níveis de certeza e deixará João bastante em dúvida quanto ao verdadeiro efeito das mudanças. Com essa nova informação, ele veria as chances de o novo sistema ser benéfico ou maléfico como praticamente iguais. Novos relatórios positivos poderiam, de fato, fazer com que ele passe a ter uma opinião positiva e menos incerta sobre o novo sistema de trânsito.

É possível mostrar também que quanto mais credibilidade uma nova evidência tiver, mais ela afetará o nível de certeza de João. Se, por exemplo, ele pensasse que o relatório fosse publicado por uma fonte imparcial (mas ainda sujeita a erro), poderia assumir que dificilmente dariam um parecer positivo à mudanças prejudiciais e atribuir Pr(P|F) = 5%. Nesse caso, João passaria a acreditar que há 89% de chances de o novo sistema ajudar a reduzir o congestionamento. (O leitor pode tentar diversas combinações de valores na fórmula acima, inclusive aplicando-a repetidamente para analisar o efeito de sucessivas evidências).

Por fim, considere um último exemplo. Pedro mora na mesma cidade de João, mas tem uma visão mais extrema. Ele tem total certeza de que as mudanças serão prejudiciais: Pr(V) = 0% e Pr(F) = 100%. Substituindo na regra de Bayes, vemos que nada acontece. As probabilidades a posteriori serão sempre iguais às a priori. Não importa a evidência, argumento ou o nível de credibilidade da fonte, nada fará Pedro mudar de ideia.

Conclusão: o excesso de confiança é uma armadilha

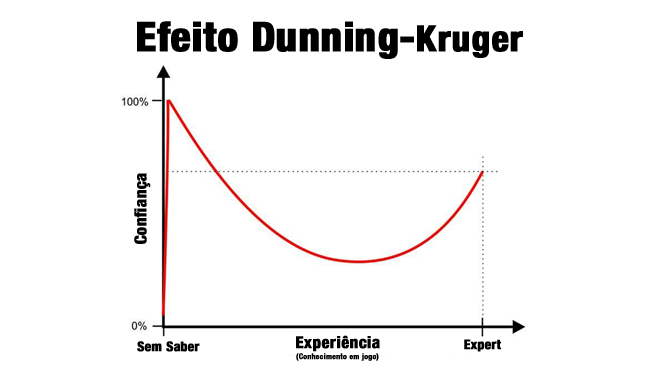
A moral da história é que se há certeza absoluta, não há atualização nem aprendizado. Ou seja, não há fatos ou argumentos que convençam quem não tem dúvidas e não cogita a possibilidade de estar enganado. O excesso de confiança em sua posição impede o indivíduo de avaliar sua própria ignorância em determinado assunto: ele sequer sabe que não sabe. Essa ideia está relacionada ao chamado Efeito Dunning-Kruger (que também tratamos aqui). Esse fenômeno pode ser resumido pelo gráfico abaixo:

Sem espaço pra dúvida, ficamos presos no vértice da total convicção e do pouco conhecimento. O progresso vem apenas quando passamos a duvidar de nós mesmos, reconhecemos nossa relativa ignorância e aprendemos com os outros. Frequentemente, nesse processo passamos a entender a complexidade de questões que antes pareciam tão simples. E, principalmente, vemos que argumentos contrários, que antes soavam absurdos e sem sentido, podem ao menos ter algum mérito.

Na próxima vez que uma questão importante exigir sua atenção e você, leitor, for expressar sua posição, pense: “que evidência me faria reconsiderar minha opinião?“. Se não houver sequer uma hipotética e improvável evidência que atenda a esse critério, cuidado! Você pode estar sendo o próximo dogmático do debate e desperdiçando uma boa oportunidade de aprendizado.

[1] Hill, Seth J. Learning Together Slowly: Bayesian Learning About Political Facts. Working paper disponível em http://www.sethjhill.com.